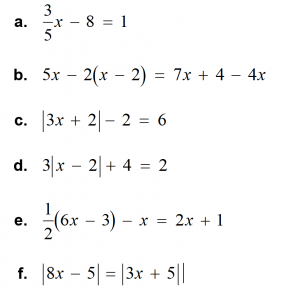Solving Linear Equations
The ability to understand and use equations is very useful in real life for events like converting between different measurements. For example, many countries measure temperature in degrees Celsius instead of degrees Fahrenheit.
Downloads & Activities
Goals
- Write and solve simple equations.
- Write and solve multi-step equations.
- Write and solve equations with variables on both sides of the equal sign.
- Write and solve absolute value equations.
- Rewrite equations to solve for one variable in terms of the other variable(s).
Vocabulary
- An absolute value equation is an equation that contains an absolute value expression.
- An equation that has two or more variables is called a literal equation.
Concepts
Addition Property of Equality
• Adding the same number to each side of an equation produces an equivalent equation.
• If a = b, then a + c = b + c.
Subtraction Property of Equality
• Subtracting the same number from each side of an equation produces an equivalent equation.
• If a = b, then a – c = b – c.
Multiplication Property of Equality
• Multiplying each side of an equation by the same number produces an equivalent equation.
• If a = b, then a · c = b · c.
Division Property of Equality
• Dividing each side of an equation by the same number produces an equivalent equation.
• If a = b, then a ÷ c = b ÷ c, c ≠ 0.
Solving Multi-Step Equations
- To solve multi-step equations, use inverse operations to isolate the variable.
Solving Equations with Variables on Both Sides
- To solve equations with variables on both sides, collect the variable terms on one side and the constant terms on the other side.
Solving Absolute Value Equations
- To solve |ax + b| = c for c > 0, solve the related linear equations ax + b = c or ax + b = –c.
Temperature Conversion
- A formula for converting from degree Fahrenheit F to degrees Celsius C is 𝐶 = 5/9 (𝐹 − 32).
Remember …
- Whatever you do to one side of the equation, you must do to the other side of the equation.
- Whenever a variable or constant term is moved from one side of the equal sign to the other, the opposite operation is used.
- Two equations that have the same solution are equivalent equations.
- Equations can have one solution, no solution or infinitely many solutions.
- When solving an equation that has no solution, you will obtain an equivalent equation that is not true for any value of the variable.
- When solving an equation that has infinitely many solutions, you will obtain an equivalent equation that is true for all values of the variable
- To rewrite a literal equation, solve for one variable in terms of the other variable(s).

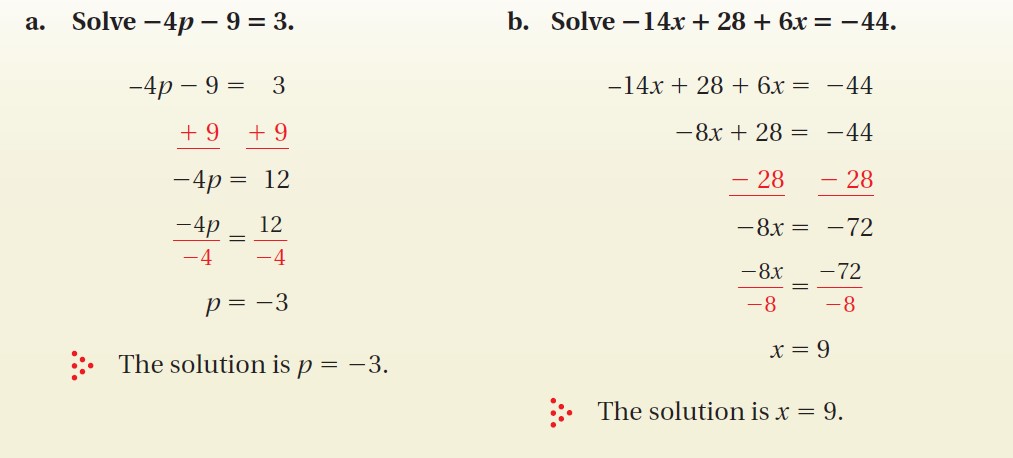


Challenge Yourself …
Which of the following equations have only one solution? Which have two solutions? Which have no solution? Which have infinitely many solutions?