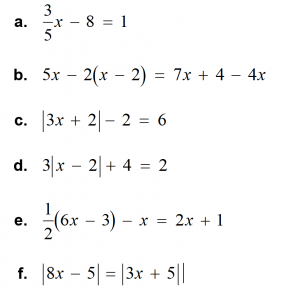Solving Linear Equations
Goals
- Solve linear equations using addition and subtraction.
- Solve linear equations using multiplication and division.
- Use linear equations to solve real-life problems.
- Solve multi-step linear equations using inverse operations.
- Use multi-step linear equations to solve real-life problems.
- Use unit analysis to model real-life problems.
- Solve linear equations that have variables on both sides.
- Identify special solutions of linear equations.
- Solve absolute value equations.
- Solve equations involving two absolute values.
- Identify special solutions of absolute value equations.
- Rewrite literal equations.
- Rewrite and use formulas for area.
- Rewrite and use other common formulas.
Vocabulary
- A conjecture is an unproven statement about a general mathematical concept.
- A proven statement about a general mathematical concept is a rule or a theorem.
- An equation is a statement that two expressions are equal.
- A linear equation in one variable is an equation that can be written in the form ax + b = 0, where a and b are constants and a ≠ 0.
- A solution of an equation is a value that makes the equation true.
- Inverse operations are two operations that undo each other, such as addition and subtraction.
- Equivalent equations are equations that have the same solution(s).
- An equation that is true for all values of the variable is an identity and has infinitely many solutions.
- An absolute value equation is an equation that contains an absolute value expression.
- An extraneous solution is an apparent solution that must be rejected because it does not satisfy the original equation.
- An equation that has two or more variables is called a literal equation.
- A formula shows how one variable is related to one or more other variables.
Concepts
Addition Property of Equality
- Adding the same number to each side of an equation produces an equivalent equation.
- If a = b, then a + c = b + c.
Subtraction Property of Equality
- Subtracting the same number from each side of an equation produces an equivalent equation.
- If a = b, then a − c = b − c.
Multiplication Property of Equality
- Multiplying each side of an equation by the same nonzero number produces an equivalent equation.
- If a = b, then a ⋅ c = b ⋅ c, c ≠
Division Property of Equality
- Dividing each side of an equation by the same nonzero number produces an equivalent equation.
- If a = b, then a ÷ c = b ÷ c, c ≠
Solving Multi-Step Equations
- To solve a multi-step equation, simplify each side of the equation, if necessary.
- Then use inverse operations to isolate the variable.
Solving Equations with Variables on Both Sides
- To solve an equation with variables on both sides, simplify one or both sides of the equation, if necessary.
- Then use inverse operations to collect the variable terms on one side, collect the constant terms on the other side, and isolate the variable.
Special Solutions of Linear Equations
- Equations do not always have one solution.
- An equation that is true for all values of the variable is an identity and has infinitely many solutions.
- An equation that is not true for any value of the variable has no solution.
Four-Step Approach to Problem Solving
- Understand the Problem
What is the unknown? What information is being given? What is being asked?
- Make a Plan
This plan might involve one or more common problem-solving strategies.
- Solve the Problem
Carry out your plan. Check that each step is correct.
- Look Back
Examine your solution. Check that your solution makes sense in the original statement of the problem.
Properties of Absolute Value
Let a and b be real numbers. Then the following properties are true.

Solving Equations with Two Absolute Values
To solve ∣ ax + b ∣ = ∣ cx + d ∣ , solve the related linear equations ax + b = cx + d or ax + b = −(cx + d).
Common Problem-Solving Strategies
- Use a verbal model.
- Guess, check, and revise.
- Draw a diagram.
- Sketch a graph or number line.
- Write an equation.
- Make a table.
- Look for a pattern.
- Make a list.
- Work backward.
- Break the problem into parts.
Steps for Solving Linear Equations
Here are several steps you can use to solve a linear equation. Depending on the equation, you may not need to use some steps.
Step 1 Use the Distributive Property to remove any grouping symbols.
Step 2 Simplify the expression on each side of the equation.
Step 3 Collect the variable terms on one side of the equation and the constant terms on the other side.
Step 4 Isolate the variable.
Step 5 Check your solution.
Solving Absolute Value Equations
- To solve ∣ ax + b ∣ = c when c ≥ 0, solve the related linear equations ax + b = c or
ax + b = − c.
- When c < 0, the absolute value equation
∣ ax + b ∣ = c has no solution because absolute value always indicates a number that is not negative.
Common Formulas
Temperature
F = degrees Fahrenheit
C = degrees Celsius
C = (F − 32)
Simple Interest
I = interest
P = principal
r = annual interest rate (decimal form)
t = time (years)
I = Prt
Distance
d = distance traveled, r = rate, t = time
d = rt
Activities
Challenge Yourself …
Which of the following equations have only one solution? Which have two solutions? Which have no solution? Which have infinitely many solutions?